Consider an aribtrary time-dependend spherically symmetric metric, \begin{align} ds^2 &= -a(t,r)dt^2 + b(t,r)dr^2 + r^2d\Omega^2. \end{align} The corresponding Einstein tensor is \begin{align} G^t_t &= -r^{-2}(1-b^{-1}[1-rb^{-1}b_{,r}]) \\ G^r_r &= -r^{-2}(1-b^{-1}[1+ra^{-1}a_{,r}]) \\ G^t_r &= -a^{-1}b^{-1}b_{,t} \\ &\cdots \end{align} For a perfect fluid the stress-energy is \begin{align} T^\mu_\nu &= (\rho+\frac{p}{c^2})u^\mu u_\nu + pg^\mu_\nu. \end{align}
To begin with, we will consider static dust, where this is simply \begin{align} T^t_t &= -c^2\rho = -\frac{c^2M_{,r}}{4\pi r^2} = -\frac{c^4}{8\pi Gr^2} R_{,r} \\ T^i_j &= 0 \end{align} where $M(r)$ is the mass within radius $r$ and $R(r)$ is the corresponding Schwartzchild radius. With this, the field equations $G^\mu_\nu = \frac{8\pi G}{c^4} T^\mu_\nu$ become \begin{align} 1-b^{-1}(1-rb^{-1}b_{,r}) &= R_{,r} \\ 1-b^{-1}(1+ra^{-1}a_{,r}) &= 0 \\ \cdots \end{align} with the solution (when requiring the metric to approach Minkowski in the distance) \begin{align} b &= \Big(1-\frac{R}{r}\Big)^{-1} \\ a &= \mathrm{e}^{-\int_r^\infty \frac1r(b-1) dr} \\ &= \mathrm{e}^{-\int_r^\infty \frac{R}{r^2}(1-\frac{R}{r})^{-1}dr} \end{align}
For a thin shell of matter, $R(r) = R_s\Theta(r-r_s)$ where $\Theta(x)$ is the Heaviside step function, resulting in \begin{align} b &= \Big(1 - \frac{R_s}{r}\Theta(r-r_s)\Big)^{-1} \\ a &= 1-\frac{R_s}{r_>} \\ \end{align} with $r_> \equiv \textrm{max}(r,r_s)$. This makes sense. The interior is flat but time dilated because it is inside the potential well of the shell. The tt-component of the metric is continuous as we cross the shell, but surprisingly the rr-component is discontinuous. This is a necessary consequence of flatness. If the scale factor $b$ were the same inside the shell as at the shell, then the circumference of the shell would be $2\pi r b$ on the inside and $2\pi r$ on the outside.
Shell with $R_s$ outside point-mass with $R_c$. \begin{align} b &= \Big(1 - \frac{R_c}{r} - \frac{R_s}{r}\Theta(r-r_s)\Big)^{-1} \\ a &= \Big(1-\frac{R_c}{r}\Big)\frac{1-\frac{R_c}{r_>}-\frac{R_s}{r_>}}{1-\frac{R_c}{r_>}} \\ \end{align}
For multiple stacked shells, where each shell has radius $r_i$ and Schwartzchild radius (for that shell alone) $R_i$, and $r_{i>} \equiv \textrm{max}{r,r_i}$, we get \begin{align} b &= \Big(1-r^{-1}\sum_i R_i \Theta(r,r_s)\Big)^{-1} \\ a &= \prod_i \frac{r_{i>} - \sum_{j\le i}R_j}{r_{i>} - \sum_{j<i} R_j} \end{align}
Of course, static dust isn't very realistic as it wouldn't stay static for long without pressure to hold it up, and would be relativistic by the time the metric becomes interesting. As an approximation to this we can consider a distribution of radially moving photons instead. In this case the 4-velocity is not defined, but we can still write the stress-energy tensor in terms of the local Schwartzchild radius. \begin{align} T^t_t &= -\frac{c^4}{8\pi Gr^2} R_{,r} \\ T^r_r &= +\frac{c^4}{8\pi Gr^2} R_{,r} \end{align} The photons will be moving, so the solution will no longer be static, but since the relevant components of the Einstein tensor do not involve time derivatives, we can find the metric independently for each time step as above. \begin{align} 1-b^{-1}(1-rb^{-1}b_{,r}) &= R_{,r} \\ 1-b^{-1}(1-ra^{-1}a_{,r}) &= -R_{,r} \end{align} which gives the same $b$ as before, but a modification to $a$. \begin{align} b &= \Big(1-\frac{R}{r}\Big)^{-1} \\ a &= \mathrm{e}^{-\int_r^\infty \frac1r (b[1+R_{,r}]-1)dr} \\ &= \mathrm{e}^{-\int_r^\infty \frac1r \Big(\frac{1+R_{,r}}{1-\frac{R}{r}}-1\Big)dr} \end{align}
For a thin shell, $R(r)=R_s\Theta(r-r_s)$, resulting in \begin{align} b &= \Big(1 - \frac{R_s}{r}\Theta(r-r_s)\Big)^{-1} \\ a &= \Big(1-\frac{R_s}{r_>}\Big)\mathrm{e}^{-\frac{R\Theta(r-r_s)}{r_s-R\Theta(0)}} \\ \end{align} Note that $a$ here depends on $\Theta(0)$ which is ambiguous. The radial profile of the thin shell matters even in the limit of zero width. For symmetric distributions (like we have used in the numerical examples) it is consistent to use $\Theta(0)=\frac12$, but asymmetric distributions will have other values.
Radially moving light follows the null-geodesic \begin{align} ds^2 = 0 = -a(t,r)dt^2+b(t,r)dr^2 \Rightarrow \frac{dr}{dt} = \pm \sqrt{\frac{a}{b}} \end{align} Hence the mass profile updates as \begin{align} R_{,t} &= R_{,r}\frac{dr}{dt} = \pm R_{,r}\sqrt\frac{a}{b} \end{align}
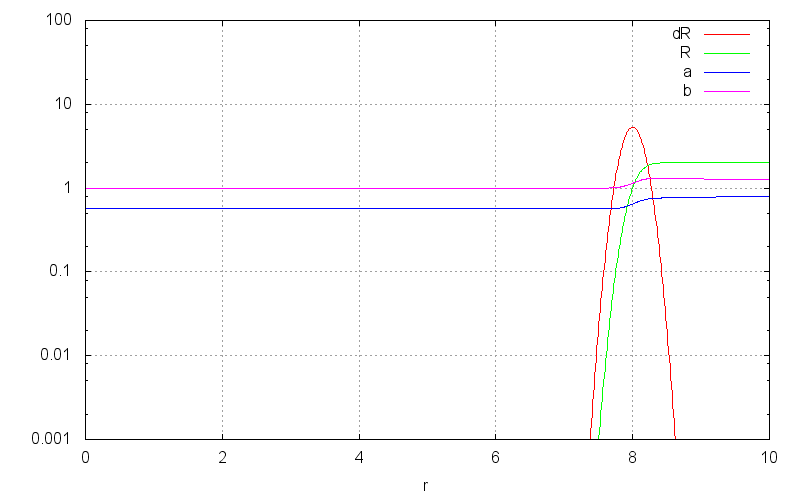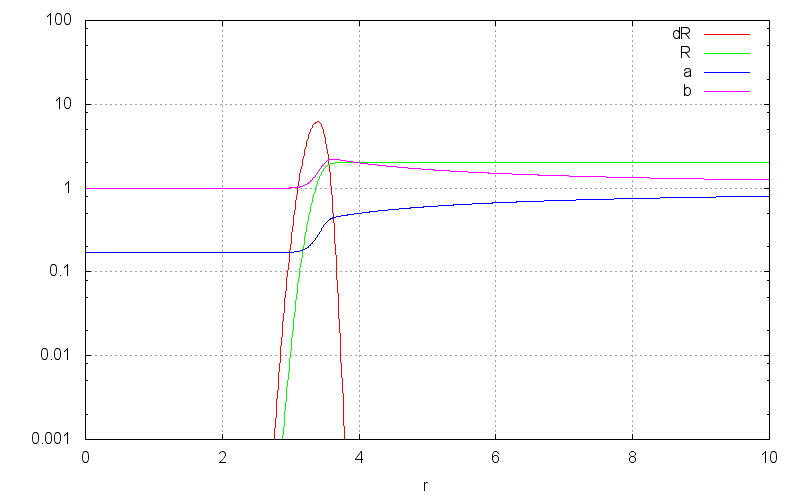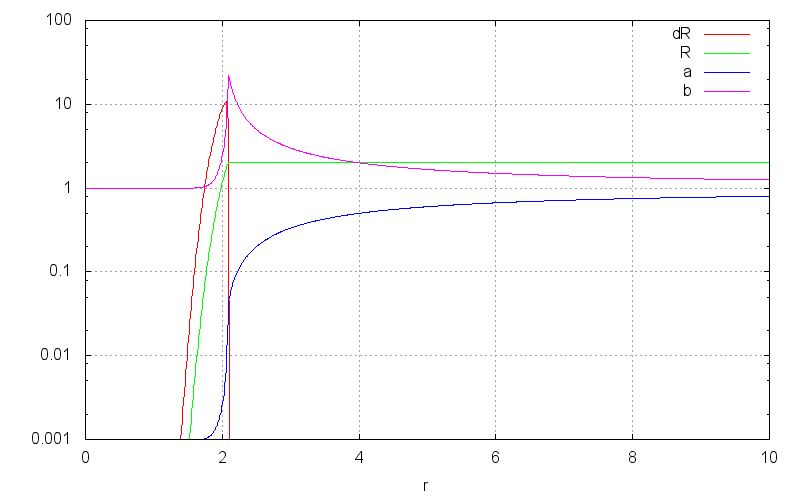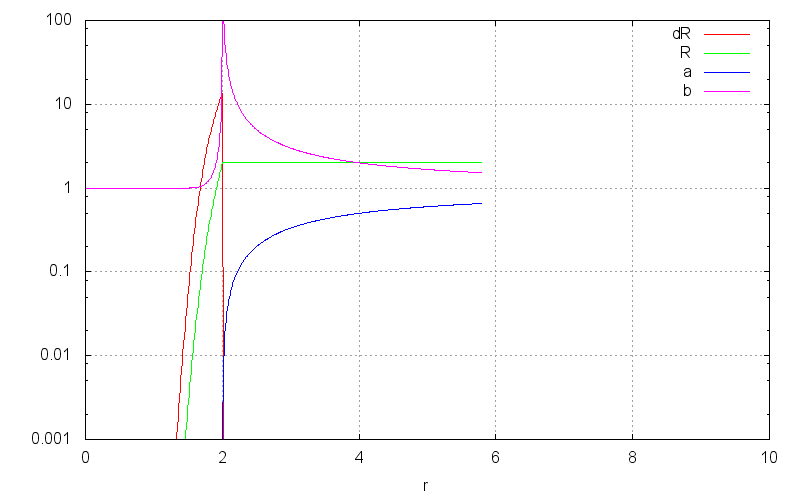
According to the Stefan-Boltzmann-Schwartzchild-Hawking law, a black hole radiates the power \begin{align} P &= \frac{\hbar c^6}{15360\pi G^2 M^2} \end{align} as seen by a far-away observer. Since the Schwartzchild radius is proportional to energy, we can express this power in Schwartzchild units, \begin{align} \frac{dR}{c dt} &= \frac{2G}{c^3}\frac{dE}{dt} = \frac{\hbar G}{1920\pi c^3 R^2} = (1920\pi)^{-1} \frac{\ell_\mathrm{P}^2}{R^2} \end{align} with the solution \begin{align} \frac{R}{\ell_\mathrm{P}} &= \left(\frac{t}{640\pi t_\textrm{P}}\right)^{\frac13} \end{align} For high radii, the Hawking radiation travel time is negligible compared to the evaporation time, and the density of hawking radiation will be negligibly small outside the horizon area. The vacuum approximation only breaks down when the radius approaches a few orders of magnitude of the Planck length $\mathcal{l}_\mathrm{P} = 1.616 \cdot 10^{-35}$m. For $r \gg \mathcal{l}_\mathrm{P}$ the metric outside an evaporating black hole is well described by the disappearing point mass approximation, \begin{align} ds^2 &= -\Big(1-\frac{R(t)}{r}\Big)dt^2+ \frac{dr^2}{1-\frac{R(t)}{r}} + r^2d\Omega^2 \end{align} But in the last few moments, the density of outgoing radiation is significant. We can model the metric here as the solution for outgoing radiation such that $dR/dt$ at a far-away point matches that of Hawking radiation.
Numerically, we can find an approximate solution for this by simulating the time-reverse of evaporation, with infalling light. The following animation shows such an evaporation simulation compared to the disappearing point mass approximation. As you can see, the approximation is excellent all the way down to holes with planck-length radii.